Joseph Farrell: "Looking at More Evidence in Antitrust"

Dear readers, the Network Law Review is delighted to present you with this month’s guest article by Joseph Farrell, Professor of the Graduate School in the Department of Economics, University of California at Berkeley.

****

Competition policy builds on a simple idea. If much more business flows to those who offer better deals, as it does in markets that we call competitive, then society is significantly immunized from any actor’s incompetence or undue greed because the incompetent or greedy won’t do much business. That fact generates incentives for efficient operation, pricing, and innovation.

If the foundational idea is so simple, why is antitrust complicated, and is that OK, or should we seek simpler implementations of the core idea? I take this opportunity to explore some very stylized analyses that help me think about those deep issues. There are obvious conventional—and real—benefits of consulting more evidence rather than simplifying and basing decisions on fewer facts and less-subtle analyses. And when a decision-maker is given more evidence and is trusted to interpret it well in a certain sense, some otherwise knotty differences of opinion expressed in differing priors and differing loss functions can be diluted and even mooted. But that is not the end of the story. A decision-maker presented with a richer and more complex record will naturally have to weigh conflicting pieces of evidence, especially in litigated cases. For reasons I explain below, that necessary activity widens the scope for other sorts of disagreements or errors, which are not encapsulated in differences of priors and loss functions and which are omitted from many standard discussions of error-cost analysis, decision theory, and Bayesian statistics.

With hindsight, some former simple and straightforward principles of yesterday’s antitrust amount to what we would now view as oversimplistic claims about economics. The world is complex, and so are many markets, so at one level, it is unsurprising and appropriate that antitrust has evolved to mirror the complexity of its subject matter. For example, the antitrust Agencies “consider all reasonably available and reliable evidence” in reviewing a horizontal merger, according to Section 2 of the 2010 Horizontal Merger Guidelines. Antitrust enforcement often calls itself “fact-specific” and hungry for evidence. And where antitrust enforcement instead cuts short the quest for evidence, as in per se or bright-line rules, it often justifies doing so by asserting that, in some class of instances, “experience shows” that looking at more (or certain kinds of) evidence is highly unlikely to move the outcome. That justification seems to concur that (subject to costs) one would ought to look at “all reasonably available” evidence if it had a real prospect of changing the decision. And that principle aligns well with the standard model of decision-making under uncertainty by a single decision-maker (DM), such as an agency or a court. In that model, as I rehearse below, more information (evidence) helps the DM make better decisions, which are more attuned to the case and are thereby more valuable.

Yet a strand in today’s turbulent antitrust Zeitgeist is a yearning for simplicity and a feeling that when decision-makers confront the mixed and complex picture that results from hearing all available evidence, something valuable is often lost. I believe this is not all advocacy and is not all aesthetics: a detailed inquiry into all aspects of an antitrust dispute can risk backburning the pro-competition presumption with which we began¹ and could expand opportunities for confusion or error by complicating the analytical agenda. Adding too many questions, even quite legitimately, can undermine the appealing fundamental simplicity and robustness with which this piece began.

So I start out with some real sympathy for a pro-simplicity view, but it is not initially obvious how more information can be harmful. This essay begins with some benefits of consulting more evidence but then identifies some rational reasons for a well-informed neutral commentator to wish to limit the evidence that an imperfect DM will see.

As such, it seeks to contribute to the vigorous, but not always rigorous, debate on how policy can best operate in a world of complexity. In antitrust, both Chicagoans and Neo-Brandeisians favor simple models and simple rules, but very different ones, while mainstream antitrust economics recognizes and may even overstate complexity. What can we say about good policy in this respect?

Beliefs and Evidence in a (Fairly) Standard Model

Consider a single decision-maker (DM) who is imperfectly informed but who is rational and sophisticated about that imperfection and about the implications of seeing more information. Such a DM is modeled as choosing a decision that maximizes his expected payoff, given the uncertainty (imperfect information) he faces, which he treats as having a subjective probability distribution. To keep the discussion relatively simple and concrete, I assume that his uncertainty concerns whether a proposed merger is anticompetitive (hypothesis A) or benign (hypothesis B). I denote by p the probability that he attaches to hypothesis A, incorporating a (relatively simple) baseline set of facts. For instance, this might incorporate the fact that it is a horizontal merger between the third and fourth largest suppliers of widgets but not yet include any deep analysis of whether “widgets” are an antitrust market or whether the merger would yield significant efficiencies. We call p the DM’s “prior” probability because it is what he believes prior to seeing the additional evidence whose consequences we are evaluating.

The DM’s decision problem also involves his loss function: a standard (if pessimistic in tone) way to represent his underlying preferences. In that representation, we normalize the DM’s payoff at zero if he makes perfect decisions (blocks an anticompetitive merger or allows a benign one), and charge him with losses L for a false positive and M for a false negative.

Assuming that both L and M are strictly positive, the DM would block the merger if p is close enough to 1, and allow it if p is close enough to 0. Specifically, he will block the merger if the expected loss from doing so is less than that from allowing it, or p. 0 + (1 – p). L < p.M + (1 – p). 0, or 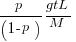. The left-hand side of this condition is called the odds ratio, and we can call the right-hand side the loss ratio. The odds ratio is a nonlinear but increasing function of p, in other words, a measure of beliefs, while the loss ratio is independent of those beliefs. Each of those ratios can potentially take any positive value.

Seeing more evidence, of course, would change the DM’s beliefs and hence potentially, his action. Acquisition of new information (more evidence) replaces the DM’s prior belief or odds ratio with a “posterior” probability or odds ratio that might be either greater or less than the prior. Those changes in belief themselves have probabilities: before seeing the evidence, it is unpredictable in which way it will point, and the posterior can be viewed as itself a random variable whose average is p: the weighted average of the DM’s posterior beliefs ought to be his prior.

Bayes’ rule tells us about those posterior beliefs. Think of both the observation x and the true hypothesis (A or B) as random variables. The joint probability of both observing x, and hypothesis A, is equal to the “likelihood” (or probability) of observing x conditional on hypothesis A, times the prior probability of A: p[A&x] = p[x|A]p[A]. Similarly, p[B&x] = p[x|B]p[A]. Taking the ratio, we have:

At the same time, we have p[A&x] = p[x]p[A|x] and similarly for B, so the left-hand side of the displayed equation is equal to :

which is the odds ratio conditional on having seen x. Thus we have Bayes’ famous rule:

In other words, the effect of observing x is multiplying the odds ratio by the “likelihood ratio,” the first factor on the right of this equation. If the observation x would be more likely under hypothesis A than under B, the likelihood ratio is greater than 1, and the observation raises the odds ratio (shifts beliefs toward hypothesis A); conversely, of course, if the observed x would be more likely under hypothesis B.²

In this overall framework, more evidence is at least weakly valuable to the DM by helping optimize his decision, making false positives and/or false negatives less likely. That fact in itself is very general and robust (within the single-chooser framework): after all, he could choose to ignore the additional evidence, which would give him the same expected payoff as if he never saw that evidence. Indeed, if the new evidence will not change his decision—for instance, if the likelihood ratio will predictably be close enough to unity to leave unchanged the comparison between the odds ratio and (L/M)—then the new evidence is of no value to the DM. By the same token, he will gain if there is a positive chance that his posterior would differ sufficiently from his prior that he would change his decision to block or allow the merger.³

A Commentator’s Views May Differ

Now introduce a commentator—one who thinks that the DM is getting things wrong. I am not focusing on an advocate or litigant who might prefer the same decision no matter the merits of the merger, but rather a sophisticated good-faith observer who wants good antitrust enforcement.

Such a commentator (or commentators) may disagree with the DM’s loss functions and prior probabilities, L, M, and p. There is certainly ample well-informed disagreement on those quantities.⁴ Those different perceptions often put daylight between what the DM decides and what a commentator would decide in light of the same explicit evidence, be that the relatively simple baseline description of the case (perhaps “an exclusive-dealing agreement” or “a largely horizontal merger”) or the expanded evidence base that includes the additional information x. But does giving the DM additional information make those disagreements more likely and more intractable, or less?

Emma’s Lemma and Bayesian Consistency

In Jane Austen’s Emma (1815), Emma and her respected friend Mr. Knightley debate whether Frank Churchill is culpable for not attending his widowed father’s second wedding. Neither Emma nor Knightley has met Churchill, and they know rather little about him. After some unproductive back-and-forth, Emma observes that they “are both prejudiced; you against, I for him; and we have no chance of agreeing till he is really here.”

Intuitively (and reading only slightly between Emma’s lines), she expects that she and her friend will have a good chance of agreeing after they meet Churchill. Thus their uncomfortable initial disagreement can be expected to fade in light of more evidence.⁵ I call this point Emma’s Lemma (the name is too tempting to resist). The idea is that after they meet Churchill, both will adjust their beliefs in the same direction, corresponding to the weightier new evidence that they will then share. And if the adjustment is large enough—the new evidence weighty enough—then any disagreement about the loss ratio would also become unimportant because their approximately-shared beliefs will be confident enough to put them in the zone where their final decisions will coincide.

The statistical topic of “Bayesian consistency”⁶ finds that, in reasonable circumstances, in the limit as more and more evidence is introduced, “the data swamp the prior” so almost any prior beliefs will evolve to almost the same posterior, a narrow penumbra of slight uncertainty surrounding a highly confident belief in the truth. If, e.g., hypothesis A is correct, then the log-likelihood ratio from each piece of evidence will, on average, be positive, so after enough pieces of evidence, the posterior log odds ratio will almost surely be large and positive (hypothesis A will be strongly supported), almost no matter what the prior. Since this applies to all observers, no matter their starting values of p or their L or M, everyone’s posterior beliefs will eventually cluster tightly near one or the other end-point and hence also near one another. Moreover, in our context, with a discrete decision (block or allow the merger) as the endpoint, neither some residual uncertainty nor a lingering slight disagreement between parties who started with different priors actually matters, nor does an ordinary difference of views about the loss ratio. That is, once everyone’s posterior probability for hypothesis A is high enough, it doesn’t matter if they disagree about whether it is 95% or 99%; nor does it matter if some think it has to exceed 90% to justify action and others would put that threshold at 70%.

However, there are a couple of twists. First, we are asking about the effects of some more evidence, not whether an almost infinite amount of more evidence (often further assumed to be essentially more draws of the same experiment) would be helpful. Second, although Bayesian consistency takes care of disagreements about p and about L and M, it assumes—as do most expositions of Bayesian logic that I have seen—that the likelihood ratio corresponding to a given observation x is objective and therefore agreed upon. (Indeed, one can think of much Bayesian statistics not as assuming a prior and deriving posterior beliefs but rather as objectively reporting likelihood ratios.) Despite the twists, however, the intuitive idea that “the data” (or evidence) may at least start to swamp initial disagreements is key to both topics.

Looking to refine the argument, I would identify two assumptions implicit in my discussion or (mutatis mutandis) in Emma’s. First, I assume that each commentator, like the DM, basically agrees with the antitrust agenda, in the sense that each prefers to block an anticompetitive merger and allow a benign one: everyone’s L and M are strictly positive. This assumption puts us in the space of good-faith policy discussion: I am not trying to model pure advocacy.⁷

Second, I assume that commentators and the DM qualitatively agree on how to interpret any potential piece of evidence. By this, I mean that they agree on the direction in which a given piece of evidence points—that is, whether it supports or undermines the hypothesis that the merger is anticompetitive, or in Bayesian terms, whether the likelihood ratio is above or below 1 (equivalently, whether the sign of the log-likelihood ratio is positive or negative). This assumption is much weaker than is standard in Bayesian decision theory, which assumes that the likelihood of an observation given a hypothesis is derived mathematically, so that there is precise agreement on the likelihoods and thus on the likelihood ratio. However, as I will argue below, my assumption is stronger than it might seem.

With those seemingly mild assumptions, there is an intuition—although no proof—that each commentator (as well as the DM) should generally support exposing the DM to more evidence. Obviously, sometimes a piece of evidence will “point the wrong way,” but that will be the exception rather than the rule.

Let me put this into the form of an internal monologue of a “progressive” commentator who believes that the DM (e.g., a court) is wrongly reluctant to block troublesome horizontal mergers. The commentator muses: “I believe the courts are way off base in their perceived loss functions (L and M) and in their subjective prior belief p about the fraction of mergers that are anticompetitive. I’ve had no luck pointing out those errors—not surprising, since it would be a challenging econometric project to pin down those quantities, and I don’t have precise estimates either. Still, I’m confident I’m more right than those courts are, so what can I do? If I encourage courts to get much more information, their beliefs will move toward one or the other endpoint, and I’m fairly confident that their beliefs will move toward hypothesis A (the merger is anticompetitive), because statistical logic says their beliefs will likely move toward the truth and because I believe that the truth is hypothesis A. I know about the identity that says that the ex ante expected value of the posterior is equal to the prior, but of course that doesn’t apply if the prior is just deluded, as I believe theirs is. I believe that the DM’s posterior p will systematically tend to increase.⁸ So more analysis and evidence could moot their mistaken prior p. (And if perchance I am wrong in my prior, I will learn something, and we know that more information for the DM is socially desirable if the DM’s prior beliefs and loss function estimates are reasonable.) As for the DM’s (in my view) off-base views on the loss ratio, if the DM looks at enough more information, its posterior and mine will be close to one of the endpoints, and so its decision will be a lot like a decision under certainty; thus its beliefs about loss functions won’t really matter.”

Why then the intractable disagreement?

Those encouraging observations might suggest that everyone of good faith would agree that adducing more evidence is good. But they don’t—so we now have a sharper version of the question, “why don’t they, then?” What’s unconvincing about the fictitious monologue above?

I believe a key issue is that commentators, rightly or not, lack faith in the DM’s interpretation of evidence—that is, in the likelihood ratio by which the DM will, versus should, modify its prior in light of additional evidence x. As noted above, this issue does not come up in many Bayesian discussions because the likelihood ratio (unlike priors) is assumed to be an objective mathematical consequence of each contending hypothesis. But even if the DM and the commentator assess different magnitudes of log-likelihood ratios for the additional evidence, that seems to leave roughly intact the intuition above provided that they agree on the direction in which that evidence points (the sign of the log-likelihood ratio). Can there reasonably be differences in the direction—that is, one observer treats evidence x as supporting hypothesis A while another treats x as supporting B?

In some cases, yes: two observers might indeed interpret a single piece of evidence in opposite directions. For instance, a familiar intuition views (sincere) complaints by rivals as a sign that a horizontal merger is pro-competitive, but an observer who believes that a larger and more powerful firm may well engage in exclusion might interpret it as the opposite. Similarly, merger efficiencies are widely viewed as pro-competitive, but even within the consumer welfare standard, some would fear that medium-run efficiencies accruing to an already powerful firm are threatening to long-run consumer welfare via a risk of less rivalry.

But more common than such directional disagreement about a narrowly defined “piece” of evidence, I suspect, is disagreement about the relative strength or informativeness of two pieces of evidence that (everyone would agree) point in opposite directions. One might distinguish between disagreements on how to weigh evidence on a particular topic or aspect of the overall inquiry versus disagreements on how to weigh the dimensions of the inquiry, although both have the same implications here.

As an example of the former, suppose that executives testify that the merged firm plans to increase R&D spending, but economic testimony indicates weakened post-merger incentives for R&D. Different fact-finders or commentators, aware of both of those pieces of evidence, might well weigh them differently. This seems distinct (though probably not sharply distinct) from a disagreement in the latter category, such as one DM thinking that most efficiencies will eventually be passed through even without much rivalry, while another thinks that mergers among direct rivals with high diversion ratios are usually harmful even if they enhance efficiency.

Either way, that kind of disagreement on relative magnitudes of opposite-sign evidence opens the door for directional disagreements about the likelihood ratio to be assigned to a given “body” (multiple “pieces”) of evidence. That is, if people agree about the signs of X and Y but disagree about their magnitudes, they can easily disagree about the sign of (X – Y). Consequently, a mixed body of evidence might shift a DM’s beliefs in one direction and a dissenting commentator’s in the opposite direction rather than partially converging as in Emma’s Lemma or Bayesian consistency. Recent Bayesian scholarship, in particular Acemoglu et al. (2016), seems to support this intuitive concern.⁹

In that framework, several plausible problems suggest themselves. Confirmation bias (over-weighting evidence that agrees with one’s prior) has more room to influence the outcome if there are more pieces of conflicting evidence. The book Merchants of Doubt describes how the presence of conflicting evidence may have led decision-makers to over-weight the “doubts” and to gravitate to a decision not to act.¹⁰ A difference in resources or in incentives to invest in winning a case can also bias the set of evidence that ends up being presented to a decision-maker.¹¹

A statistics-inspired approach is apt to (though it need not) be inspired by the case in which “pieces” of evidence either represent repeated draws of a random variable whose distribution depends on the prevailing hypothesis or at least (as in the R&D incentives illustration above) bear on the same specific part of an overall inquiry. In antitrust analysis, there is typically also another issue: different pieces of evidence often concern different dimensions of the overall inquiry that are substantively related to one another in a variety of ways. For instance, in analyzing a merger, there might be evidence of diversion ratios, previous industry attempts to collude, efficiencies, entry, buyer power, and so on. Combining and weighing these categories of evidence involves economic (and/or perhaps legal) analysis in a way that at least feels very different from weighing conflicting evidence on “the same” topic. For instance, how should one gauge the overall likelihood ratio from learning that a proposed merger would undo a lot of direct rivalry between the merging firms but that entry is not unusually difficult? That question is not very much like combining the conflicting evidence on R&D effects discussed above, but it too can turn differences in quantitative assignment of weights into a directional disagreement about net evidence.

This pattern, too, can cause trouble. There is an often-credited would-be syllogism that if, for example, the presence of some entry barriers is economically a necessary condition for competitive harm, then a plaintiff ought to have to prove the presence of entry barriers.¹² But, of course, not everything that is true is convincingly provable. An old observation is that “absence of evidence is not evidence of absence.”¹³ From a statistical point of view, it can be—but it is not likely to be conclusive evidence of absence.

Suppose, to illustrate, that when there are, in fact, entry barriers, there is a probability t ≤ 1 that the plaintiff will prove it to the standard required (some readers will recognize this as the “power” of the test). Suppose also for simplicity that there are no convincing but incorrect “proofs,” implying that the likelihood ratio from seeing a proof is infinite. However, the likelihood ratio from seeing no proof is not zero but 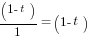. If the prior odds ratio for hypotheses A and B is 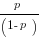, the odds ratio posterior to seeing the plaintiff fail to prove entry barriers is therefore 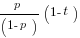. Requiring such proof, in the sense of deciding for the defendant in the absence of such proof, would forcibly “round down” the posterior to zero. When 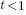, that is incorrect as a matter of inference or (viewed differently) mandates a decision that can easily differ very substantially from the optimal one given correct inference. Even if the DM has a good sense of t (and I think an intuitive grasp of statistical power issues is by no means widespread), the correct inference is not very transparent if expressed in probabilities rather than in odds ratios: the posterior probability of hypothesis A, conditional on seeing no proof of entry barriers, becomes 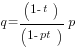. As an arithmetic example, suppose that a plaintiff is otherwise well along toward showing harm, p = 4/5, and entry barriers would likely but not surely be demonstrable if they exist, t = ¾. Then we would get q = 1/2, so treating q as zero would be a substantial misstep.¹⁴

The gap between truth and proof widens if one side, say the plaintiff, is given the burden of proof in multiple such dimensions: then, the risk of a false negative can grow significantly.¹⁵ As an arithmetic example, if the probability t of finding a proof of any one dimension or required element, conditional on the merger in fact being anticompetitive, is ¾, and there are four such dimensions, the risk of this kind of false negative grows to 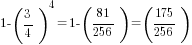≈0.68. Thus, adding more detailed “off-ramps” for defendants is not harmless from a decision-theory or error-cost standpoint.

Indeed, the risk of false negatives from decision rules that require multiple proofs from a plaintiff can easily outweigh the reduction in false positives. Importantly, this applies even if each element is, in fact, essential for competitive harm, in which case (in my experience) many antitrust practitioners and commentators are tempted to quickly infer that a plaintiff should prove each element.

To understand this in our baseline decision theory model, suppose that a DM identifies N essential elements for actual anticompetitive effect. Illustratively, for some DMs, these might include direct rivalry between the merging firms, the presence of some entry barriers, the minimal scope for repositioning, and the absence of large marginal-cost efficiencies. Although each element is assumed here to be essential for the anticompetitive effect, the same is not automatically true for proof of each element. Suppose that when a given element is, in fact, true, the plaintiff has a probability t of proving it (as above, this is the power of the “prove it!” test for that element), whereas when the element is false, the plaintiff has a presumably lower probability s of inaccurately “proving” it (in hypothesis-testing language, s is the “size” of that element-specific test).

Consider a rule that blocks a merger only if the plaintiff proves all N elements. If hypothesis A (anticompetitive merger) is true, then it will be correctly diagnosed with probability 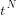, and thus missed with probability 1– 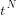, so false negatives contribute 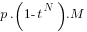to the overall expected loss. If hypothesis B is, in fact, true (the merger is benign), then it will be incorrectly diagnosed (a false positive) with probability 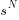, so false positives contribute 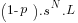to overall expected loss. Total expected loss is thus:

Another possible rule would lighten the proof requirement by requiring only proof of at least 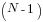of the N elements. Would that less rigorous rule lead to a higher or lower expected loss? Under this rule, the expected loss is:

The change in the expected loss from lightening the proof burden is thus:

This change is negative (relaxing the rule lowers expected loss) if:

,which is the case for all sufficiently large N provided s < t < 1. That condition for the change to lower the expected loss can be helpfully rewritten as:

The left-hand side is the posterior odds ratio if the plaintiff has proven exactly N – 1 of the N elements. The condition is telling us that if that posterior is sufficiently strongly in favor of hypothesis A such that blocking the merger would be optimal notwithstanding failure to prove (distinct from the falsity of!) one of the N elements, then any rule that requires proof of all N is not optimal and should be relaxed.

Expressed that way, the point becomes obvious: in the decision-theory model, there is no benefit in committing ex-ante to making choices that are not optimal ex-post. Yet, as I noted, it is common to hear assertions of (and relatively rare to hear pushback on) an incorrect syllogism: that if harm is unlikely absent condition C, then a plaintiff should be required to prove condition C.

Conclusion

There are real benefits of looking at more evidence, which can not only directly improve decisions but also moot certain disagreements about priors and loss functions. But the standard decision-theory model assumes that additional information will be optimally used and thereby overstates the case. Correctly interpreting mixed evidence or “absence of evidence” can be a subtle problem of statistical inference, and there is scope for good simplifications to help.

Even so, I am not ready to recommend leaving informative evidence on the shelf: rather, as an optimist, I would urge decision-makers to minimize the risks by recognizing and seeking to avoid or adjust for them. One step toward doing so, perhaps itself a simplification, is to protect the simple foundational assumptions of antitrust while seeking a new generation of simple rules and principles that encapsulate, rather than ignoring lessons from modern economics.

Joseph Farrell

As will be evident, this essay is more than usually incomplete and tentative, but I have learned a lot in the process of writing it. I thank the editor and Jonathan Baker, Aaron Edlin, Steven Salop, and Carl Shapiro for helpful comments, but they are not to be blamed for any errors nor for any of the omissions.

***

Citation: Joseph Farrell, Looking at More Evidence in Antitrust, Network Law Review, Spring 2023.

Related Posts